Kesebangunan Bangun Datar

 Kesebangunan Bangun Datar

Apa itu kesebangunan? Dua benda dikatakan sebangun apabila memiliki bentuk yang sama. Dua benda yang kongruen pasti sebangun, tetapi dua benda yang sebangun belum tentu kongruen. Kesebangunan dapat dinyatakan dengan simbol $\sim $

Syarat dua buah benda sebangun adalah:

1. Sudut yang bersesuaian sama besar
2. Perbandingan sisi yang bersesuaian senilai

Perhatikan gambar berikut!

Berdasarkan gambar di atas, maka:

Sudut yang bersesuaian sama besar yaitu $90^{\circ}$

$\frac{panjang gambar 1}{panjang gambar 2}$ = $\frac{4 cm}{2 cm} $= 2

$\frac{lebar gambar 1}{lebar gambar 2}$ = $\frac{4 cm}{2 cm} $= 2

Jadi berdasarkan pernyataan di atas sudut-sudut yang bersesuaian sama besar yaitu $90^{\circ}$ dan perbandingan sisi yang bersesuaian sama yaitu 2, maka gambar 1 $\sim$ gambar 2

Menentukan Sisi-Sisi dan Sudut-Sudut yang Bersesuaian

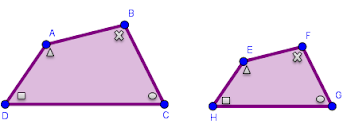
Perhatikan gambar dua bangun yang sebangun berikut ini!

Berdasarkan gambar di atas tentukan:

a. Sisi-sisi yang bersesuaian

b. Sudut-sudut yang bersesuaian

Penyelesaian:

Sisi-sisi yang bersesuaian                            Sudut-sudut yang bersesuaian

AD $\to$ EH                                                 $\angle$ A $\to$ $\angle$ E     

AB $\to $ EF                                                 $\angle$ B $\to$  $\angle$ F 

BC $\to $ FG                                                 $\angle$ C $\to$  $\angle$ G

CD $\to $ GH                                                $\angle$ D $\to$  $\angle$ H

Menentukan Panjang Sisi dan Besar Sudut yang Belum Diketahui Dari Dua Bangun Datar Sebangun

1. Perhatikan gambar berikut ini!

Bangun ABCD dan EFGH sebangun, Tentukan:

a. Nilai x, y, dan z

b. Panjang sisi EF dan BC

Penyelesaian:

a. Karena ABCD dan EFGH sebangun maka:

m$\angle $ A = m$\angle$ E

m$\angle $ B = m$\angle$ F

m$\angle $ C = m$\angle$ G

m$\angle $ D = m$\angle$ H

m$\angle $ C = m$\angle$ G $\to$ 22,6$^{\circ}$

m$\angle $ H + m$\angle $ G + m$\angle $ F + m$\angle $ E = 360 $^{\circ}$  (jumlah besar sudut dalam segi empat)

m$\angle $ H + 22,6$^{\circ}$ + 90$^{\circ}$ + 90$^{\circ}$ = 360$^{\circ}$

m$\angle $ H + 202,6$^{\circ}$ = 360$^{\circ}$

m$\angle $ H = 157,4$^{\circ}$

Jadi nilai x, y, z berturut-turut adalah 22,6$^{\circ}$, 157,4$^{\circ}$, 157,4$^{\circ}$

b. Karena ABCD dan EFGH sebangun maka:

$\frac{EF}{AB}$ = $\frac{FG}{BC}$ = $\frac{GH}{CD}$ = $\frac{EH}{AD}$

$\frac{EF}{AB}$ = $\frac{EH}{AD}$ 

$\frac{EF}{16 cm}$ = $\frac{15 cm}{20 cm}$ 

20 x EF = 16 x 15

20 EF = 240

EF = 12 cm

$\frac{FG}{BC}$ = $\frac{EH}{AD}$ 

$\frac{20 cm}{BC}$ = $\frac{15 cm}{20 cm}$ 

15 x BC = 20 x 20

15 BC = 400

BC = 24$\frac{2}{3}$