Kekongruenan Bangun Datar

 Kekongruenan Bangun Datar

Apa itu Kesebangunan?

Dua benda dikatakan kongruen apabila memiliki ukuran dan bentuk yang sama. Kekongruenan dapat disimbolkan dengan $\cong$ .

Dari contoh tersebut terlihat bahwa ukuran panjang dan lebar gambar 1 sama dengan ukuran panjang dan lebar gambar 2. Bentuk gambar 1 sama dengan bentuk gambar 2. Maka gambar 1 $\cong$  gambar 2.

Syarat Kesebangunan

1. Sisi yang bersesuaian sama panjang.
2. Sudut yang bersesuaian sama besar.

Cara Penulisan Dua Bangun Datar yang Kongruen

Cara penulisan dua bangun datar yang kongruen adalah dengan menyesuaikan nama sudut-sudut yang bersesuaian. Misalnya sudut A bersesuaian dengan sudut P, sudut B bersesuaian dengan Q, sudut C bersesuaian dengan sudut R, sudut D bersesuaian dengan sudut S. Maka penulisannya menjadi: 

ABCD $\cong$  PQRS atau BCDA$\cong$  QRSP

Perhatikan Gambar Berikut!

Jika sudut C bersesuaian dengan sudut R dan Sisi AD bersesuaian dengan sisi PS. Maka buktikanlah ABCD$\cong$ PQRS.

Sudut-sudut yang bersesuaian:

Sudut A dan Sudut P maka m$\angle$ A = m$\angle$ P

Sudut B dan Sudut Q maka m$\angle$B = m$\angle$Q

Sudut C dan Sudut R maka m$\angle$C = m$\angle$R

Sudut D dan Sudut S maka m$\angle$D = m$\angle$S

Sisi-sisi yang bersesuaian

AD dan PS maka AD = PS

AB dan PQ maka AB = PQ

BC dan QR maka BC = QR

CD dan RS maka CD = RS

Karena ABCD memenuhi kedua syarat kesebangunan yaitu sudut-susudt yang bersesuaian sama besar dan sisi-sisi yang bersesuaian sama panjang maka  ABCD$\cong$ PQRS.

Menentukan Panjang Sisi dan Besar Sudut yang Belum Diketahui

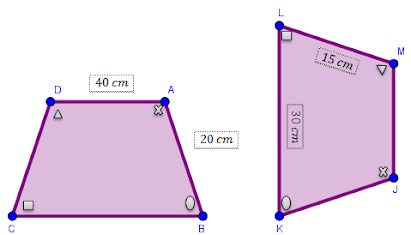
Perhatikan gambar trapesium ABCD dan trapesium JKLM yang kongruen berikut ini!

1. Jika panjang sisi AD = 40 cm, AB = 20 cm, LM = 15cm, dan KL = 30 cm. Maka tentukan panjang sisi BC, CD, JK, dan JM!
2. Jika besar m$\angle$A = 60, m$\angle$D = 40. Berapakah besar $\angle$L dan $\angle$K!

Jawab!

ABCD $\cong$ JKLM, maka:

AB = JK                m$\angle$A = m$\angle$J

BC = KL               m$\angle$B = m$\angle$K

CD = LM              m$\angle$C = m$\angle$L

AD = JM               m$\angle$D = m$\angle$M

BC = KL = 30 cm, CD = LM = 15 cm, JK = AB = 20 cm, JM = AD = 40 cm

m$\angle$A = m$\angle$J = 60 

$\angle$J + $\angle$K = 180 (dalam sepihak)

60 + $\angle$K = 180

$\angle$K = 180 - 60

$\angle$K = 120

m$\angle$D = m$\angle$M = 40

$\angle$M + $\angle$L = 180 (dalam sepihak)

40 + $\angle$L = 180

$\angle$L = 180 - 40

$\angle$L = 140