Beautiful Math
Hallo para pembaca! Selamat datang di blog beautiful math. Blog ini akan membantu kalian memahami materi matematika kelas IX semester 2. Selamat membaca yaa... salam matematika itu Indah!!
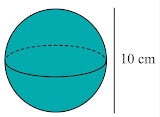
Bola
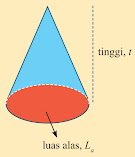
Kerucut
Unsur-Unsur Kerucut
- Memiliki dua sisi $\left ( alas dan selimut \right )$
- Memiliki tinggi
- Memiliki garis pelukis $\left ( s\right )$
- Memiliki satu titik sudut
- Memiliki jari-jari
Menentukan Luas Selimut Kerucut
Menentukan Luas Permukaan Kerucut
Menentukan Volume Kerucut
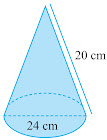
Menghitung Luas Permukaan Kerucut
Menentukan Volume Kerucut
Tabung
Unsur-Unsur Tabung
- Memiliki 3 buah sisi $\left ( alas, tutup, selimut \right )$
- Memiliki 2 rusuk
- Memiliki jari-jari
- Memiliki diameter
- Tidak memiliki titik sudut
Menentukan Luas Selimut Tabung
Mendapatkan Rumus Luas Pemukaan Tabung
Menentukan Volume Tabung
Kesebangunan Dua Segitiga
Kesebangunan Segitiga
Dua buah segitiga dikatakan sebangun apabila memiliki bentuk yang sama. Syarat dua segitiga sebangun adalah:- Sudut-Sudut yang bersesuaian sama besar
- Perbandingan sisi-sisi yang bersesuaian sama
Pehatikan gambar berikut ini!Sudut-sudut yang bersesuaian:m$\angle A$ = m$\angle A'$ (terlihat dari kode pada gambarm$\angle B$ = m$\angle B'$ (terlihat dari kode pada gambarm$\angle C$ = m$\angle C'$ (terlihat dari kode pada gambarJadi sudut-sudut yang bersesuain sama besar
Perbandingan sisi-sisi yang bersesuaian:$\frac{AB}{A'B'}$ = $\frac{AC}{A'C'}$ = $\frac{BC}{B'C'}$$\frac{6 m}{6a cm}$ = $\frac{5 cm}{5a cm}$ = $\frac{4 cm}{4a cm}$$\frac{1}{a}$ = $\frac{1}{a}$ = $\frac{1}{a}$Jadi perbandingan sisi-sisi yang bersesuaian sama
Karena segitiga ABC dan A'B'C' memenuhi syarat kesebangunan yaitu sudut-sudut yang bersesuaian sama besar dan perbandingan sisi-sisi yang bersesuaian sama, maka $\Delta$ ABC $\sim$ $\Delta$ A'B'C'
- Sudut-Sudut yang bersesuaian sama besar
- Perbandingan sisi-sisi yang bersesuaian sama
Kesebangunan Khusus dalam Segitiga Siku-Siku
Perhatikan gambar di atas!Jika $\Delta$ ABC $\sim$ $\Delta$ DBA, $\Delta$ ABC $\sim$ $\Delta$ DAC, dan $\Delta$ DBA $\sim$ $\Delta$ DAC, maka:$AB^{2}$ = BD x BC$AC^{2}$ = CD x CB$AD^{2}$ = BD x CD
Menghitung Panjang Sisi dan Besar Sudut yang Belum Diketahui dari Dua Segitiga Sebangun
Perhatikan gambar di bawah ini!Tentukan:a. Panjang sisi DE dan ABb. besar $\angle ACB$, $\angle ADE$, dan $\angle DAE$
Penyelesaian:Gambar di atas berhimpit artinya $\Delta ABC$ $\sim$ $\Delta ADE$, maka:$\frac{AB}{AD}$ = $\frac{AC}{AE}$ = $\frac{BC}{DE}$
a. $\frac{AC}{AE}$ = $\frac{BC}{DE}$$\frac{4 cm}{12 cm}$ = $\frac{5 cm}{DE}$4 x DE = 12 x 54 DE = 60DE = 15 cm
$\frac{AB}{AD}$ = $\frac{AC}{AE}$$\frac{AB}{AB+5 cm}$ = $\frac{4 cm}{12 cm}$12 x AB = 4 (AB + 5)12 AB = 4 AB + 2012 AB - 4 AB = 208 AB = 20AB = 2, 5 cm
Kesebangunan Bangun Datar
Kesebangunan Bangun Datar
- Sudut yang bersesuaian sama besar
- Perbandingan sisi yang bersesuaian senilai
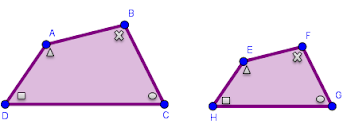
Perhatikan gambar berikut!
Menentukan Sisi-Sisi dan Sudut-Sudut yang Bersesuaian
Menentukan Panjang Sisi dan Besar Sudut yang Belum Diketahui Dari Dua Bangun Datar Sebangun
Kekongruenan Bangun Datar
Kekongruenan Bangun Datar
Apa itu Kesebangunan?
Dua benda dikatakan kongruen apabila memiliki ukuran dan bentuk yang sama. Kekongruenan dapat disimbolkan dengan $\cong$ .
Dari contoh tersebut terlihat bahwa ukuran panjang dan lebar gambar 1 sama dengan ukuran panjang dan lebar gambar 2. Bentuk gambar 1 sama dengan bentuk gambar 2. Maka gambar 1 $\cong$ gambar 2.
Syarat Kesebangunan
- Sisi yang bersesuaian sama panjang.
- Sudut yang bersesuaian sama besar.
Cara penulisan dua bangun datar yang kongruen adalah dengan menyesuaikan nama sudut-sudut yang bersesuaian. Misalnya sudut A bersesuaian dengan sudut P, sudut B bersesuaian dengan Q, sudut C bersesuaian dengan sudut R, sudut D bersesuaian dengan sudut S. Maka penulisannya menjadi:
Menentukan Panjang Sisi dan Besar Sudut yang Belum Diketahui
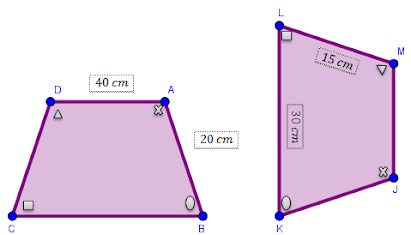
- Jika panjang sisi AD = 40 cm, AB = 20 cm, LM = 15cm, dan KL = 30 cm. Maka tentukan panjang sisi BC, CD, JK, dan JM!
- Jika besar m$\angle$A = 60, m$\angle$D = 40. Berapakah besar $\angle$L dan $\angle$K!
Kekongruenan Segitiga
Kekongruenan Dua Segitiga
Seperti yang sudah kita pelajari sebelumnya, dua buah bangun dikatakan kongruen apabila:
- Sisi-sisi yang bersesuaian sama panjang
- Sudut-sudut yang bersesuaian sama besar
- Sisi-sisi yang bersesuaian sama panjang
- Sudut-sudut yang bersesuaian sama besar
Bola
Unsur-Unsur Bola Bola adalah bangun ruang sisi lengkung yang dibentuk dari tak hingga lingkaran yang memiliki jari-jari sama panjang dan be...

-
Kesebangunan Segitiga Dua buah segitiga dikatakan sebangun apabila memiliki bentuk yang sama. Syarat dua segitiga sebangun adalah: Sudut-Su...